Explanation of why subtracting has the same effect as adding a negative, and how rewriting addition as subtraction allows terms to be easily re-arranged. Introduction to the use of the word “term” in algebra, along with how terms may be re-arranged.
Tag: Algebra
Algebra Intro 6: Multiplication
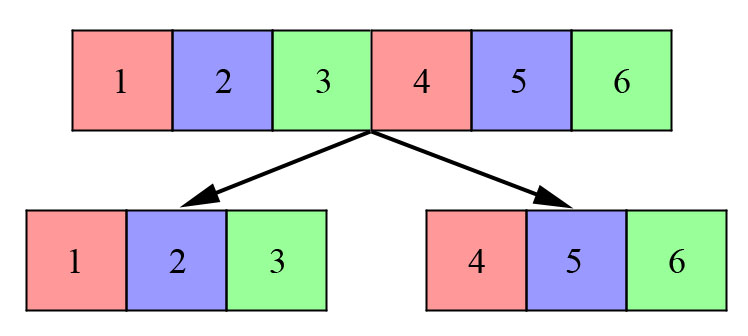
We have all known our multiplication tables for years, and have successfully answered questions like “what is 6 times 7?”, but do we really understand what multiplication represents? Repeated Addition One interpretation of multiplication, which only works when multiplying by an integer, is “repeated addition”. From this perspective, “6 times 7” is a compact way to…… Continue reading Algebra Intro 6: Multiplication
Algebra Intro 7: Properties of Multiplication
Properties Of Multiplication Do the patterns that applied to addition also apply to multiplication… do the following all produce the same result? $latex 3 \cdot 5 \cdot 7 \\*~\\*3 \cdot (5 \cdot 7) \\*~\\*(3 \cdot 5) \cdot 7&s=2&bg=ffffff&fg=000000$ After carefully following the order of operations, we see that they all result in a value of 105.…… Continue reading Algebra Intro 7: Properties of Multiplication
Algebra Intro 8: Division
The last “arithmetic” operation introduced in school is usually division. While multiplication allows us to calculate the total needed for a group when a fixed quantity is required for each person, division allows us to determine how much each person will get when a fixed quantity is divided equally among all in a group. …… Continue reading Algebra Intro 8: Division
Algebra Intro 9: Fractions, Reciprocals, and Properties of Division
Exploration of fractions as ratios, division problems, and the inverse of multiplication. What they look like, what they mean, and their lack of algebraic properties (associative, commutative).
Algebra Intro 10: Fractions and Multiplication
Exploration of ways to think about, and approach, fractions that are useful when working with them. What does a product of fractions mean, and what alternatives are there for evaluating it?
Algebra Intro 11: Dividing Fractions, Equivalent Fractions
Once a person is comfortable with multiplying fractions, dividing one fraction by another becomes fairly straightforward. Dividing Fractions An alternative to division by any number (not just a fraction) is “multiplying by the reciprocal”. Dividing by two has the same effect as multiplying by one half. Multiplying by the reciprocal of a number will always produce…… Continue reading Algebra Intro 11: Dividing Fractions, Equivalent Fractions
Algebra Intro 12: Adding and Subtracting Fractions
Once someone knows how to multiply fractions, and is comfortable creating equivalent fractions by multiplying by a fraction that equals 1, they have to tools needed to add and subtract fractions. Why Can’t I Just Add Two Fractions As Written? Consider the fraction “two thirds.” The phrase as written can be represented in two ways:…… Continue reading Algebra Intro 12: Adding and Subtracting Fractions
Summary: Algebra
When faced with an algebraic expression or equation, there are only two types of things you can do to it without changing the quantitative relationship that it describes. Re-write one or more terms in an equivalent form This can be done to any expression (no equal sign) or equation (with an equal sign) at any…… Continue reading Summary: Algebra
What Is Algebra?
Algebra is a combination of: A notation system for representing quantitative relationships, andA set of rules for manipulating notation without changing the underlying quantitative relationship that it represents. Why is algebra needed? Because: The notation provides a concise and commonly accepted way of accurately communicating quantitative relationships, andChanging the appearance of the notation describing a relationship,…… Continue reading What Is Algebra?
Operations are taught in pairs
Many High School students I have worked with have not spent much time pondering the sequence in which math topics were taught to them. So, it can be interesting to step into the “waaay-back” machine and investigate this question a bit: What was the very first arithmetic operation you were taught (probably in first grade)? What…… Continue reading Operations are taught in pairs