Sigma (Summation) Notation
The Sigma symbol, , is a capital letter in the Greek alphabet. It corresponds to “S” in our alphabet, and is used in mathematics to describe “summation”, the addition or sum of a bunch of terms (think of the starting sound of the word “sum”: Sssigma = Sssum).
The Sigma symbol can be used all by itself to represent a generic sum… the general idea of a sum, of an unspecified number of unspecified terms:
But this is not something that can be evaluated to produce a specific answer, as we have not been told how many terms to include in the sum, nor have we been told how to determine the value of each term.
A more typical use of Sigma notation will include an integer below the Sigma (the “starting term number”), and an integer above the Sigma (the “ending term number”). In the example below, the exact starting and ending numbers don’t matter much since we are being asked to add the same value, two, repeatedly. All that matters in this case is the difference between the starting and ending term numbers… that will determine how many twos we are being asked to add, one two for each term number.
Sigma notation, or as it is also called, summation notation is not usually worth the extra ink to describe simple sums such as the one above… multiplication could do that more simply.
Sigma notation is most useful when the “term number” can be used in some way to calculate each term. To facilitate this, a variable is usually listed below the Sigma with an equal sign between it and the starting term number. If this variable appears in the expression being summed, then the current term number should be substituted for the variable:
Note that it is possible to have a variable below the Sigma, but never use it. In such cases, just as in the example that resulted in a bunch of twos above, the term being added never changes:
The “starting term number” need not be 1. It can be any value, including 0. For example:
That covers what you need to know to begin working with Sigma notation. However, since Sigma notation will usually have more complex expressions after the Sigma symbol, here are some further examples to give you a sense of what is possible:
Note that the last example above illustrates that, using the commutative property of addition, a sum of multiple terms can be broken up into multiple sums:
And lastly, this notation can be nested:
The rightmost sigma (similar to the innermost function when working with composed functions) above should be evaluated first. Once that has been evaluated, you can evaluate the next sigma to the left. Parentheses can also be used to make the order of evaluation clear.
Pi (Product) Notation
The Pi symbol, , is a capital letter in the Greek alphabet call “Pi”, and corresponds to “P” in our alphabet. It is used in mathematics to represent the product of a bunch of terms (think of the starting sound of the word “product”: Pppi = Ppproduct). It is used in the same way as the Sigma symbol described above, except that succeeding terms are multiplied instead of added:
Summary
Sigma (summation) and Pi (product) notation are used in mathematics to indicate repeated addition or multiplication. Sigma notation provides a compact way to represent many sums, and is used extensively when working with Arithmetic or Geometric Series. Pi notation provides a compact way to represent many products.
To make use of them you will need a “closed form” expression (one that allows you to describe each term’s value using the term number) that describes all terms in the sum or product (just as you often do when working with sequences and series). Sigma and Pi notation save much paper and ink, as do other math notations, and allow fairly complex ideas to be described in a relatively compact notation.


am very thankful 2 the information above.it is very helpful to me
I always see these equations on in technical papers but I never knew how to decode them. This was so helpful! It’s basically a for loop in scripting, makes so much sense. Also your blog is awesome, thank you for sharing!
Thank you! And yes, a little programming experience with loops makes Sigma and Pi Notation much easier to understand…
Very very useful. Thanks a lot – Sundaram
Thank you, this was very helpful. I was finding how to use Sigma notation, and finally found such a good one.
Indeed a very lucid exposition of Sigma and Pi notations! Thanks 🙂
Very useful post. But what if the Pi notation is not in closed form, such as
If the index limit above the Pi symbol is a variable, as in the example you gave:
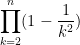
then there are an indeterminate number of factors in the product until such time as “n” is specified.
I suppose a problem could be posed this way if you are being asked to come up with an expression for such a product that does not involve Pi notation: is there some closed form expression involving “n” that represents this product?
So, if n=3, then
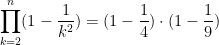
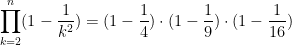
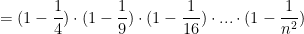
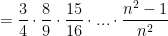
and if n=4, then
and if you leave the final index as “n” becomes:
Is there some closed form expression that represents this product?
Shouldn’t the k be squared ?
Which “k” are you referring to? There are several in the posting… Ooops – I just realized you were asking about my reply to the comment. You are correct. I will modify my response shortly.
Actually n SHOULD be squared in his reply since he’s saying that that’s the LAST TERM in the product. Basically this is where k = n. It’s important to emphasize that.
what is the relation between the two when they are logarithmic differentiated?
It would help if you could provide an example of what you are asking about.
If you need to differentiate a sum, I would not expect logarithmic differentiation to be very useful, as the laws of logarithms do not allow us to do anything with something like
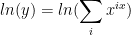
Differentiating this would turn the right side into the reciprocal of the original sum times its derivative = a mess.
However, if you need to differentiate a product, logarithmic differentiation could make life simpler by converting a long succession of product rule applications into a sum of logs. Since
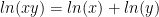
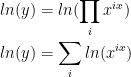
we can rewrite the log of a product as a sum of logs:
which, in many cases, could simplify the differentiation process.
If sigma is for summation, and pi is for multiplication, are there any notations for division and subtraction? Just out of curiosity?
Good question!
Subtraction can be rewritten as the addition of a negative. So Sigma notation describes repeated subtraction when its argument is a negative quantity.
Division can be rewritten as multiplication by the reciprocal. So Pi notation describes repeated division when its argument has a denominator other than 1.
Therefore, additional notations are not needed to describe repeated subtraction or division… Which is quite convenient.
Sir, how about expressing thing one 1x2x3 + 2x3x4 + 3x4x5 + ….will it be a combination of
sigma and pi? If you can illustrate it please.
You are correct – this can be represented using a combination of Sigma and Pi notation:
In the above notation, i is the index variable for the Sum, and provides the starting number for each product. By having the Product index variable start at zero, the expression to generate each value is a bit simpler. If j went from one to three each time, the expression on the right would have to be (i + j – 1).
hello sir,
thank you for the amazing and very helpful post.
I was just practicing the question wanted to know can 30….. n(n+1)(n+2) be the ans to the above sigma and product equation given by you.
hope to receive your reply as soon as possible.
Gargi,
The Sigma and Pi expression I used to answer the previous question did not have a value specified for “N”, so any value given for the expression will have to be in terms of “N”… as your question is. However, your expression leaves me uncertain as to whether you are analyzing the situation correctly or not.
Let’s list the first few terms of this sequence individually to get a sense of how this series behaves:
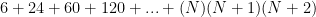
So, the sum of the first two terms would indeed be 30. But if you are trying to give a general answer, you should show each term individually so that the person reading your answer can see any pattern that is developing, and understand how to fill in the “…” used to represent all the terms that are not shown.
Hi Mr. Ford,
any hint for the solution of following infinite series will appretiated.
Thanks…
Yucel,
Evaluating the first few terms, just to get a sense of its behavior, produces the following (after converting all fractions to have a common denominator so that they are easier to compare quickly:
i=0: (14/12)
i=1: (14/12)(8/12)
i=2: (14/12)(8/12)(6/12)
i=3: (14/12)(8/12)(6/12)(5/12)
It seems that successive terms are growing smaller, since each is the previous term multiplied by a factor that is less than 1 and shrinking, so the series will converge (it shrinks faster than a geometric sequence with a common ratio that is less than one). But to what value?
I don’t know what context this problem arises in for you, and therefore what tools you are expected to use to analyze the problem (assuming it is a problem from a class). Plus I have not worked with infinite series in a while – off the top of my head, I might try to “squeeze” this between two series for which I know the sum, to at least provide upper and lower bounds for the sum. An upper bound would be provided by an infinite geometric sequence, but I am uncertain what might best provide a lower bound.
Does that help?
what can be the correct answer this equation?
The example was an expression, not an equation, therefore it cannot be “solved”. However, this particular example can be “simplified” by collecting like terms to become
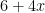
 ?”. My answer to that would be: I probably would not use Sigma Notation to write such a simple expression. This example was intended show how to interpret Sigma Notation in some of the many ways that it can be used.
?”. My answer to that would be: I probably would not use Sigma Notation to write such a simple expression. This example was intended show how to interpret Sigma Notation in some of the many ways that it can be used.
which would raise the question: “why write it using Sigma Notation when you could just as easily write
We can also write as …
∑(n=0)^3▒〖n+∑(n=0)^3▒x〗
Good suggestion – it makes more sense to keep the expression the same as the previous example! I have modified the post.
I have a student asking whether there is a symbol for exponentiation of a sequence? So there’s SIGMA for summation of a sequence, PI for multiplication of a sequence and perhaps something else for exponentiation of a sequence?
So like E(x+n) for n=1 to 3 would produce (x+1)^(x+2)^(x+3)… Or maybe((x+1)^(x+2))^(x+3)
Thanks,
Jonty
Jonty,
Good question! I am not aware of such notation, and furthermore, I am not aware of situations where such notation would be needed. Do you know of situations that require repeating exponentiation to model them? I suppose that some multi-dimensional models (perhaps like String Theory) could require some repeated exponentiation, but even there I doubt they would need to get beyond several levels of exponentiation (the result would grow really fast…).
I’ll research this a bit to see if I can find anything, and if I do I’ll post another reply.
Thanks Whit. The student in question is actually only 11 years old and somehow I don’t think that he will accept the “not needed” reason! I’ll challenge him to find a need for it and maybe he can create his own notation. He said it had something to do with his investigation into combination formulae… He’s currently using a backwards SIGMA symbol!
Jonty,
One other thought… if
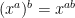
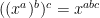
and therefore
etc…
then there is no need for a notation to represent repeated exponentiation, since exponents that are products already represent repeated exponentiation. Using Pi notation in the exponent achieves the desired purpose.
Good point, however, x^a^b is not the same as x^ab. For repeated exponentiation I would assume that form rather than (x^a)^b. So maybe we do still need something?
Ooops – didn’t think of
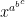
I still cannot think of either an application for such an expression or a notation for it. Perhaps this is a good question for a forum like http://math.stackexchange.com/questions
If the sum of a bunch of terms in known as a “summation of a series”, then what is the product of a bunch of terms known as in mathematics?
The exact vocabulary used is likely to differ from one person to another, and I doubt that everyone will care that much about the words used, but I will be picky about the words used in an effort to clarify the situation and answer your question.
A “sequence” is an ordered set of terms which are NOT added together. There is often a pattern to them, a formula that can be used to determine the value of the next term in the sequence. Sequence definitions usually have no need for summation notation.
A “series” is the sum of the first N terms of a sequence. Series definitions almost always rely on summation notation.
The phrase you wrote, “summation of a series”, is either redundant (they could have just said “a series”), or indicated that they wish to sum the first N terms of a series (the sum of terms, each which is a sum, something that might have a use, but I have not seen used).
A polynomial (such as a quadratic) can be called “a sum of terms”.
And finally to your question. A “product” is the result of multiplying two or more “factors”. The entire product is a single “term”.
So when using pi notation, the expression after the pi describes each “factor” (not “term”), and the final result after the pi notation has been evaluated is a “product”. No new vocabulary is needed.
Does Multiplication operator always increment? does work?
work?
i.e. can there be a bigger value at the base and smaller value at top of the PI operator? I want to do that to signify that the matrices do not commute.
Interesting question! Notation is a convention, a commonly shared interpretation of some symbols. So, even if it is not commonly used in a particular way, there is no strong reason I can think of why you couldn’t use it that way (if necessary, including a note or example describing how you intend the notation to be interpreted).
Loops in programming languages can be written to decrease the index each time just as easily as they can increase it. The convention is to increase it, just like with Sigma and Pi notation, but they also support decreasing indeces.
So, my opinion would be: sure! Why not? If I were to see an upper index value that is smaller than the lower one, my first assumption would be that I would need to decrease the index by 1 for each iteration – which seems to be what you intend.
I do not follow your thinking though when you say you wish to use a descending index value to indicate that matrices do not commute… I would not perceive a descending index value, or an ascending one, to indicate anything about the commutative property’s applicability to the resulting expression. After expanding the Pi notation into the full expression that it represents, the person working with that expression must follow the rules of algebra (or matrix algebra), and the index number of each factor would not have any effect on such rules. But, perhaps I do not understand the situation you seek to describe.
I like it … And I hope it will help other students too to acheive their goals …
How can u write this using summation notation: 3 -5+7 -9+11-13+15?
Appiah,
I notice three things when I look at this sequence:
1) The values alternate sign, so we need a factor that changes sign for each value of “n”. (-1)^n will change sign every time “n” grows by one, but when n=1 it is negative – which is the wrong sign for the first time. Adding or subtracting 1 from “n” will make the factor positive when n=1 (since a negative raised to the zero, or an even, power is positive). So will provide the correct sign for the nth term.
will provide the correct sign for the nth term.
2) The values grow in magnitude linearly by 2 each time. A factor of (2n) will produce such numbers, but when n=1 this will have a value of 2, not 3… so I need to add 1 to each value: .
.
3) There are seven terms, so n will need a starting value of 1, and an ending value of 7.
Putting the three thoughts above together, I get:
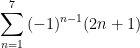
What if I want to write the sequence:
using Sigma or Pi notation, or possibly both. Furthermore is there a way of simplifying the notation and finding a result that is a function of n?
If I have interpreted the expression you show correctly, it is neither an arithmetic nor a geometric sequence. Futhermore, it appears to me as though it will always have an infinite number of sub-expressions that need to be evaluated, regardless of the value of “n”.
It is not
– a sum of consistent terms (the third term contains all the of the remaining “terms”)
– a product of consistent factors (the first two terms are not multiplied by what follows)
so I do not see a way of representing it using either Sigma or Pi notation.
You may be able to simplify this expression by expanding the values a bit to see if there is a pattern, but the result will probably vary a great deal depending on the value of “n”. For example, if n=1, then the expression would be:
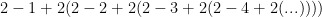
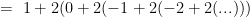
it would appear as though the quantity in parentheses is becoming increasingly negative (a sum of growing negative numbers), and therefore the value probably goes to negative infinity.
If n=2, then
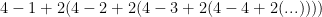
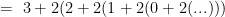
once again it would appear as though the quantity in parentheses is going to become increasingly negative (a sum of growing negative numbers), and therefore the value propably goes to negative infinity again, even though it starts out a bit larger.
As n grows, the constant power of 2 in the expression will dominate the initial results a lot more, but the infinite number of subtractions from it will eventually catch up to its value, no matter how large it is.
Thanks for your clear explanations. It helps me to understands the notation means and how to use it.
Hello,
How would I derive the polynomial for the following expression:
n = 112
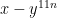
expression is
multiply until n reaches 143 (i.e. n=112, n=113 etc.)
I’m interested in simplifying the polynomial to 32 terms and determine the exponents of y
Thank you.
Alin,
Using Pi notation, I interpret your question to be
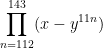
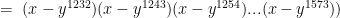
Using a binomial expansion, the terms will be
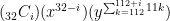
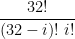
for i = 0 to 32. Terms with odd values of i will be negative.
The coefficients will be “32 Choose i”, or
Does that help?
Hello, I am trying to utilize the Pi notation to represent a repeating multiplication, but one that rounds up to the nearest whole after each time there is a multiplication(or division). Before I continue please forgive my mathematical illiteracy, I am taking an amateur interest in this.
What I am wondering about is this. If I wanted to take, let’s say “I”, and multiply “I” by a repeating multiple, let’s say “1/(1-r)”.
I might write it as: I×(1÷(1-r))×(1÷(1-r))×(1÷(1-r))… or I÷(1-r)÷(1-r)÷(1-r)…
Reading this post it seems like this would be easy to use the big Pi Π notation.
Ex: I × Π(1÷(1-r))….. something like that.
If I wanted to represent something being rounded up I think I could use ceiling function brackets: ⌈⌉. So for instance, if I wanted to round the above to the nearest whole after each division (or multiplication) step I think I could write: ⌈⌈⌈I÷(1-r)⌉÷(1-r)⌉÷(1-r)⌉…. In my mind, this rounds up each time the value is divided by (1-r). I simply cannot figure out how to represent that using big Pi Π.
I hope that makes some sense.
Any insights would be very appreciate.
Thanks,
Brad
Brad,
The notation that follows a capital Pi describes only the term that is to be multiplied. The difficulty you describe is that you wish to specify what happens to the result of that product, and capital Pi notation does not provide any means to do that.
Two ways to resolve the problem come to mind:
1) your expansion of the problem using square brackets
2) using a programming language to describe a loop in which each product is then rounded, before repeating the loop until the specified number of multiplications have been carried out.
Hello,
Sir,If I have equation like this :
X1=(1-P1)(1-P2)P3+(1-P2)(1-P3)P1+(1-P3)(1-P1)P2
X2=(1-P1)P2.P3+(1-P2)P2P3+(1-P3)P2P3
X3=P1.P2.P3
For example, X1 means we have One term say P3 and rest two are (1-P) and summation of such product terms for 3 values(P1,P2 and P3).
How should I proceed if I want to get it for n instead of 3.
Equation for Xn in terms of P1,P2,……Pn.
Summation notation does not provide an easy way that I can think of to do what you describe. While it can add a bunch of terms very nicely, the challenge is describing each of the terms you show as a function of the term number. This would be easy to do in a computer program, but not so much using summation notation.
limit,n–>infinity {tan(p/2n)tan(2p/2n)tan(3p/2n)……}^(1/n) . find the value where p=pi. option (a) 1 (b) 2-log2 (c) 3 (d) 3 -log4. please reply in my email ( dpaswan309@gmail.com). thanks
Dharmendra,
This problem is not strictly a Pi Notation problem, as it involves a limit and a power outside of any Pi Notation.
Also, I am not certain where the product you describe is supposed to end. If it ends with, or continues beyond tan(np/2n), which will always be undefined, then my first impression is that there would be no limit to the product. However, I have never worked with infinite products. Your answer options suggest that there is some expansion of a a logarithm that results in an infinite product of tangent functions, however I am not familiar with that.
Sorry!
How to find the derivative of the pi notation
If each factor described by the pi notation contains an instance of a the variable, you would need to use the product rule… potentially many times. However, if each factor does not contain the variable (or a function of the variable) that you are differentiating with respect to, then the whole product would be a constant. So, depending on the number of factors in the product, it could be a very long process, or a very short one.
Best explanation sir.
I have a question, please.
Is there a way to rewrite the following expression using both sigma and pi?
Ln =4 (1+ 1/3 + 8/9 + (8^2) / (3^3) +…+ (8^(n-1)) / (3^n))
I think this would do it. Pi is not needed:
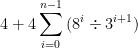
Thank you. The post was tremendously helpful
Sir, this is a very helpful website. Excellent blog and makes maths symbols and operations simple to understand. Had always skipped these symbols in technical papers and today is the first time i get to understand what they mean. Now i will not skip them anymore when i come across them in papers. I will always be checking this site.
Thank you greatly for this blog! Appreciate the details as I struggle with math, so to see a full text explanation and all the examples really helps me to understand.
What is a capital S notation?
I am not familiar with capital S notation. Can you provide me with a link to an example where it is being used?
Try this. If it doesn’t work, I can email you a screenshot that somebody sent me on facebook.
It looks like that is an integral sign (calculus), given the “dx” at the end of the expression.
You’re right. I didn’t see it at first. Should there be brackets around the expression? It looks like the dx applies only to the numerator.
No brackets needed for that expression, given that the numerator is in parentheses. Or, the dx can be written just to the right of the fraction line (be sure to leave a little space…) and that will have the same effect as putting brackets around the whole fraction.
Thanks for taking the time to chat with this retired math teacher who hasn’t seen calc since I walked out of my last final college exam.
I plugged it into this generator and it produced – 2.98 approximately. Doesn’t seem correct considering it’s supposed to be a 4 digit pin number.
https://www.integral-calculator.com/
My TI-84 calculator has a numerical integration result of -2.582086699. My techniques of integration are a bit rusty, but I could not see a way to integrate it by hand using u-substitution. It factors into (x-1)(3x^2+2x+4) / sqrt[(x-1)(x-2)] but that does not seem to help much either. So I let my calculator do the work.
Thank you Sir for this explanation. I would like to know how to write the expression (1+2)+(1+2+2²)+(1+2+2²+2³)+…(up till n terms) using sigma notation. I’d also like to know its solution. Thanks in advance.
I would start by rewriting each term (in general) as
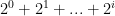
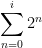
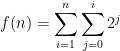
which can be shortened using Sigma Notation to
then to add up all the terms you indicate, add another Sigma outside of this
From there, you ask what its solution is. You have provided an expression, which would produce a different result for each value of n – so there is no “solution”. However, there might be a “closed form”, which produces f(n) with less calculation than evaluating all the Sigmas. To find this, write down the first few results, and look for a pattern. There is no fixed procedure for doing this – it’s like a puzzle to solve. Some expressions may be able to be summarized in a simpler (and easier to evaluate) formula, while others cannot:
f(1) = 3
f(2) = 3 + 7 = 10
f(3) = 3 + 7 + 15 = 25
f(4) = 3 + 7 + 15 + 31 = 56
Do you see any pattern in the above expressions or results that would allow you to calculate them with a shorter/simpler formula?
Thanks. What I meant by a “solution” was an algebraic form that could be seen as the ‘generalised sum up till n terms’.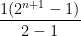 i.e.,
i.e., 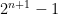 . However, I don’t know how to write this sigma algebraically now. I was told that it can be simplified as
. However, I don’t know how to write this sigma algebraically now. I was told that it can be simplified as 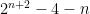 , but was unable to get to that. Recently, I got to know my mistake and now have successfully simplified it down. Thanks for the support
, but was unable to get to that. Recently, I got to know my mistake and now have successfully simplified it down. Thanks for the support
I can see the first sigma as a Geometric Progression’s sum. So, it can be written as
Yes, the Nth term of a Geometric Series can be found using the formula:
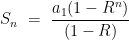
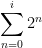
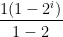
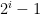 (a slightly different exponent than you indicated in your message)
(a slightly different exponent than you indicated in your message)
This can be used to find the value of the “inner” Sigma from my previous post
by applying the formula for the sum
or in simplified form
So we are now left to evaluate the outer Sigma, which now looks like
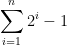
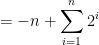
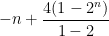
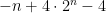
 (as you indicated in your message)
(as you indicated in your message)
but the -1 is present in every term, and can be pulled out of the Sigma as a (-n)
making it possible to apply the formula for the sum of a Geometric Sequence a 2nd time to the expression above and obtain
which simplifies to
which in turn simplifies to
f(n) =
And testing this formula against the values in my original reply shows that it works: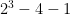 = 3
= 3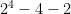 = 10
= 10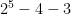 = 25
= 25 = 56
= 56
f(1) =
f(2) =
f(3) =
f(4) =
Fantastic Post ! Sir, I have just learn from you that There is also a term PI that use for Series of Multiplication like Sigma is for Summation… Sir, I have a question … I am currently Researching a new idea in Recreational Mathematics… The idea is basically a Formula for any given Integer that has to be processed in special way … I am ilustrating it with an Example…
For example 66 is an integer… It can be processed with this formula:
Formula= Integer that having digits XYZ upto Nth digit so, [ {X+Y+Z+Nth}{(XY)+(YZ)+(ZNth)}…… You can Call it as Direct Cipher or simply DC for easy understanding…… Rules are if integer has any zero digit in it then it will be attached to the left Non-zero value, evaluation will be ended when duplicate value found or a 2 digit value received with 0 in it like 90…… Some integers contains special characteristics like 58 with no evaluation and reversing effect ]…… Example: 66 if taken as initial integer then it gives you 432 in the first hand, if do a chain then 432 gives you 162 and then further 162 gives you 162 again…… so for initial integer 66, 162 is a constant [162 acts as final cipher and 432 acts as first cipher]…..
I have explained the Formula above and how to process it with an example of 66 integer … Integer can be any as a starting value so it has a First DC and Final DC… Sir, I believe that this formula can be expressed with both Notations SIGMA and PI combinations… But I don’t know how? Help needed in this regard… Thanks in Advance…
Mr. Fraz,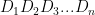 .
.![[\displaystyle\sum_{i=1}^{n} D_{i}]*[\displaystyle\sum_{i=1}^{n-1} (D_{i}*D_{i+1}]](https://s0.wp.com/latex.php?latex=%5B%5Cdisplaystyle%5Csum_%7Bi%3D1%7D%5E%7Bn%7D+D_%7Bi%7D%5D%2A%5B%5Cdisplaystyle%5Csum_%7Bi%3D1%7D%5E%7Bn-1%7D+%28D_%7Bi%7D%2AD_%7Bi%2B1%7D%5D&bg=ffffff&fg=000&s=0&c=20201002)
From your question, if each digit of a number is represented as a subscripted D, then the number would be
Your formula becomes
However, this notation DOES NOT take your rule about 0 into account, or the repeated application of the formula until an unchanging value is arrived it. To do that, it would be easier to write a short piece of computer code.
As often as I’ve seen Sigma used in that notation, unbelieveably I’d never seen Pi! Many thanks!!