This post begins a series intended to help introduce or re-introduce some of the core concepts of Algebra. It is often very helpful to re-visit these concepts with students who may have memorized their way through previous math courses without slowing down to contemplate some of the concepts behind Algebra.
Numbers
Numbers are used in the English language as both nouns and adjectives. However, the only physical instance of a “number” in our world is a symbol or group of symbols such as “23”. Most of the time, we seem to use numbers as adjectives: “Look at the two trees.”
Adjectives represent concepts or ideas: small, large, thin, thick, few, many, green, red, rough, slippery, two, twelve. Adjectives are not objects in our world that we can physically manipulate. We can think about them, write down the word that represents them, illustrate them in graphical ways, and manipulate our thoughts, words, or illustrations based on them… but we cannot touch them. All numbers are abstractions, concepts, a fabrication of the mind.
That does not prevent us from finding ways of representing them though… piles of objects, or marks on the ground or on paper are frequently used to represent numbers.
Another common way of graphically or visually representing a number is by using a number line. A number line consists of a straight line marked at equal intervals. Each mark has a number written below it, allowing a number to be physically located on the line relative to other numbers being discussed. By convention, larger numbers are placed to the right, and smaller numbers to the left, using a consistent scale. The quantities being illustrated are highlighted by shading a region of the line, or if only one quantity is being illustrated, by drawing a dot.
Algebra
Algebra is the exploration of ways we can manipulate expressions that describe quantitative relationships, in much the same way that an English course explores how to manipulate words. Algebra lets us change the way an expression or equation looks, without changing the quantitative relationship that it represents.
Algebra no doubt arose from people seeking to analyze and understand quantitative problems in their world. While many topics in mathematics were explored in great depth long before today’s notation was invented, it could be somewhat awkward to describe a problem, let alone solve it. Over the centuries, as mathematicians worked on increasingly complex problems they gradually developed more compact notations. The notation we use today is concise and, more importantly, consistently interpreted worldwide.
Variables
In English we use pronouns to save time while communicating, particularly when we have a complex object to refer to. “It” is much easier and faster to say than “that new building two blocks down the street on the right that is painted blue”. In Algebra, variables play the role of pronouns in English. Variables refer to a specific quantity just as pronouns refer to a specific noun.
However, as people explore numerical patterns or relationships, they often stop explicitly linking them to their world… that can sometimes get in the way of exploring a pattern. This means that you will often see a variable, such as “x”, used without any explanation of what it refers to.
Note that variables are usually, but not always, used to refer to quantities we don’t know… that’s why they are called “vary”ables – the value they represent can vary. Variables can also be used to refer to quantities we do know, but which are no fun to write down exactly… such as .
Examples of quantities variables can often refer to include:
t is the amount of time that has elapsed since I woke up this morning
m stands for the number of manhole covers
h refers to the height of the building above the ground
d is the distance I have walked today
n stands for the number of cookies I need to bake today
is the measure of one angle in a triangle
Posts that continue this series:
Algebra Intro 2: Addition
Algebra Intro 3: Subtraction
Algebra Intro 4: Negative Numbers, Zero, Absolute Values, and Opposites
Algebra Intro 5: Addition, Subtraction, and Terms
Algebra Intro 6: Multiplication
Algebra Intro 7: Properties of Multiplication
Algebra Intro 8: Division
Algebra Intro 9: Fractions, Reciprocals, and Properties of Division
Algebra Intro 10: Fractions and Multiplication
Algebra Intro 11: Dividing Fractions, Equivalent Fractions
Algebra Intro 12: Adding and Subtracting Fractions


You want to be a little careful here: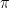 is a constant and so not a variable. Since the numerical value for
is a constant and so not a variable. Since the numerical value for 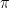 is impossible to write down, we have given it an arbitrary name, but it will never vary… it is a measured quantity that is fixed.
is impossible to write down, we have given it an arbitrary name, but it will never vary… it is a measured quantity that is fixed.
Tom – thank you for pointing out my inconsistency – I have modified the list of sample variables to use alpha instead of pi. I wanted to include at least one non-roman letter to show that Roman letters are not the only ones used as variables, and must have had pi on the mind.